Materi, Soal dan Pembahasan Super Lengkap Limit Tak Hingga (Soal UTBK SBMPTN, SIMAK UI,UM UGM dan UNDIP)

Salam Para Bintang

Berikut ini saya akan membagikan soal tentang limit tak hingga. Sudah paham dengan limit tak hingga?? Soal-soal tersebut diambil dari berbagai sumber referensi, termasuk dari soal Ujian Nasional, soal UTBK SBMPTN, dan soal tingkat olimpiade. Para pecinta matematika khususnya siswa/i yang ingin sekali belajar diharapkan sudah menguasai teori limit fungsi aljabar dan trigonometri.

Nah kita akan bahasa satu persatu, simak dengan baik ya !!

A. Limit di Ketakhinggan Fungsi Alajabar

Limit di ketakhinggan Fungsi Aljabar ada 2 yaitu :

$1.Bentuk\, \, \lim_{x\rightarrow \infty }\frac{f(x)}{g(x)}=\frac{\infty }{\infty }=Tak \, \, Tentu$

Untuk menyelesaikan limit tak hingan dengan bentuk umumnya dapat diselesaiak dengan cara membagi setiap unsur pada pembilang (f(x)) dan penyebut g(x) dengan pangkat teringgi (derajat) dari elemen pada pembilang dan elemen pada penyebut.

Dengan menggunakan rumus/konsep berikut yaitu:

$\lim_{x\rightarrow \infty }\frac{ax^{n}+bx^{n-1}+.....+c}{px^{m}+qx^{m-1}+.....+r}=L$

maka hasilnya adalah:

$L=0 , \, \, untuk\, \, n<m\, (pangkat \, \, tertinggi\, \, pembilang\, \, lebih\, \, kecil \, \, dari\, \, pangkat \, \, tertinggi \, \, penyebut)$

$L=\frac{a}{p}, \, \, untuk\, \, n=m\, (pangkat \, \, tertinggi\, \, pembilang\, \, sama \, \, dengan \, \, pangkat \, \, tertinggi \, \, penyebut)$

$L=\infty , \, \, untuk\, \, n>m\, (pangkat \, \, tertinggi\, \, pembilang\, \, lebih\, \, besar \, \, dari\, \, pangkat \, \, tertinggi \, \, penyebut)$

Dengan menggunakan Teorema bahwa:

$\lim_{x\rightarrow \infty }\frac{a}{x^{n}}=0$

Contoh 1:

Tentukan nilai dari:

$a.\lim_{x\rightarrow \infty }\frac{2x^{4}-3x^{3}+2x-6}{4x^{4}+6x^{3}+2x^{2}-x+10}$
$b.\lim_{x\rightarrow \infty }\frac{3x^{3}-3x^{2}+2x}{4x^{4}+6x^{3}+2x^{2}-x+10}$
$c.\lim_{x\rightarrow \infty }\frac{3x^{3}-3x^{2}+2x}{2x^{2}-x+10}$

Penyelesaian:

$\lim_{x\rightarrow \infty }\frac{2x^{4}-3x^{3}+2x-6}{4x^{4}+6x^{3}+2x^{2}-x+10}=\lim_{x\rightarrow \infty }\frac{\frac{2x^{4}}{x^{4}}-\frac{3x^{3}}{x^{4}}+\frac{2x}{x^{4}}-\frac{6}{x^{4}}}{\frac{4x^{4}}{x^{4}}+\frac{6x^{3}}{x^{4}}+\frac{2x^{2}}{x^{4}}-\frac{x}{x^{4}}+\frac{10}{x^{4}}}$

Dengan menggunakan Teorema bahwa:

$\lim_{x\rightarrow \infty }\frac{a}{x^{n}}=0$

maka:

$\lim_{x\rightarrow \infty }\frac{2x^{4}-3x^{3}+2x-6}{4x^{4}+6x^{3}+2x^{2}-x+10}=\frac{2-0+0-0}{4+0+0-0+0}$

$\lim_{x\rightarrow \infty }\frac{2x^{4}-3x^{3}+2x-6}{4x^{4}+6x^{3}+2x^{2}-x+10}=\frac{2}{4}$

$\lim_{x\rightarrow \infty }\frac{2x^{4}-3x^{3}+2x-6}{4x^{4}+6x^{3}+2x^{2}-x+10}=\frac{1}{2}$

$\lim_{x\rightarrow \infty }\frac{3x^{3}-3x^{2}+2x}{4x^{4}+6x^{3}+2x^{2}-x+10}=\lim_{x\rightarrow \infty }\frac{\frac{3x^{3}}{x^{4}}-\frac{3x^{2}}{x^{4}}+\frac{2x}{x^{4}}}{\frac{4x^{4}}{x^{4}}+\frac{6x^{3}}{x^{4}}+\frac{2x^{2}}{x^{4}}-\frac{x}{x^{4}}+\frac{10}{x^{4}}}$

Dengan menggunakan Teorema bahwa:

$\lim_{x\rightarrow \infty }\frac{a}{x^{n}}=0$

maka:

$\lim_{x\rightarrow \infty }\frac{3x^{3}-3x^{2}+2x}{4x^{4}+6x^{3}+2x^{2}-x+10}=\frac{0-0+0}{4+0+0-0+0}$

$\lim_{x\rightarrow \infty }\frac{3x^{3}-3x^{2}+2x}{4x^{4}+6x^{3}+2x^{2}-x+10}=\frac{0}{4}$

$\lim_{x\rightarrow \infty }\frac{3x^{3}-3x^{2}+2x}{4x^{4}+6x^{3}+2x^{2}-x+10}=0$

c.
$\lim_{x\rightarrow \infty }\frac{3x^{3}-3x^{2}+2x}{2x^{2}-x+10}=\lim_{x\rightarrow \infty }\frac{\frac{3x^{3}}{x^{3}}-\frac{3x^{2}}{x^{3}}+\frac{2x}{x^{3}}}{\frac{2x^{2}}{x^{3}}-\frac{x}{x^{3}}+\frac{10}{x^{3}}}$

Dengan menggunakan Teorema bahwa:

$\lim_{x\rightarrow \infty }\frac{a}{x^{n}}=0$

maka:

$\lim_{x\rightarrow \infty }\frac{3x^{3}-3x^{2}+2x}{2x^{2}-x+10}=\frac{3-0+0}{0-0+0}$

$\lim_{x\rightarrow \infty }\frac{3x^{3}-3x^{2}+2x}{2x^{2}-x+10}=\frac{3}{0}$

$\lim_{x\rightarrow \infty }\frac{3x^{3}-3x^{2}+2x}{2x^{2}-x+10}=\infty$

Contoh 2: SOAL UGM 2018

$Diketahui\, \, m \, \, adalah\, \, sisa\, \, pembagian\, \, polinomial\, \, h(x)=x^{3}-x^{2}+2x+2\, \, oleh \, \, x-1. \, \, Nilai \, \, k \, \, yang\, \, memenuhi \lim_{x\rightarrow \infty }\left ( \frac{mx^{3}-kx+5}{kx^{3}+3x^{2}-7}-k \right ) =0\, \, adalah....$

Penyelesaian:

$h(x)=x^{3}-x^{2}+2x+2\, \, : \, \, x-1. \, \,memiliki \, \, sisa \, \, m \, \, sehingga \, \, diperoleh\, \, :$

$m=h(1)=1^{3}-1^{2}+2(1)+2=4$

$Untuk\, menentukan \, nilai\, k,maka\, kita \, subsitusi\, nilai\, m=4\, ke:$

$\lim_{x\rightarrow \infty }\frac{mx^{3}-kx+5}{kx^{3}+3x^{2}-7}-k=0$

$\lim_{x\rightarrow \infty }\frac{4x^{3}-kx+5}{kx^{3}+3x^{2}-7}-k=0$

$\frac{4}{k}-k=0$

$4-k^{2}=0$

$k^{2}=4$

$k=\pm 2$

Jadi, diperoleh nilai k = 2 dan k = -2

$2. Bentuk\, \lim_{x\rightarrow \infty }\sqrt{ax^{2}+bx+c}-\sqrt{px^{2}+qx+r}=\infty -\infty \, (Tak \, Tentu)$

Limit dengan bentuk di atas dapat diselesaikan dengn caa mengalikan sekawannya atau dengan menggunakan rumus:

$\lim_{x\rightarrow \infty }\sqrt{ax^{2}+bx+c}-\sqrt{px^{2}+qx+r}=L$

maka:

$\blacksquare \, \, L=\infty ,untuk\, a>p$

$\blacksquare \, \, L=-\infty ,untuk\, a<p$

$\blacksquare \, \, L=\frac{b-p}{2\sqrt{a}} ,untuk\, a=p$

Untuk bentuk yang lain bisa ditentukan rumusnya yaitu :

a. Ketakterhinggaan Selisih Bentuk Linear dalam Tanda Akar

$\lim_{x\rightarrow \infty }\sqrt{ax+b}-\sqrt{px+q}=L$

maka diperoleh nilai L yaitu:

$\blacksquare \, \, L=\infty , untuk\, a>p$

$\blacksquare \, \, L=-\infty , untuk\, a<p$

$\blacksquare \, \, L=0, untuk\, a=p$

b. Ketakterhinggaan Selisih Bentuk akar pangkar tiga

$\lim_{x\rightarrow \infty }\sqrt[3]{ax^{3}+bx^{2}+cx+d}-\sqrt[3]{px^{3}+rx^{2}+sx+t}=L$

maka diperoleh hasil limit yaitu:
$L=\frac{b-q}{3\, \, \sqrt[3]{a^{2}}},untuk\, a=p$

Baca Juga:

Contoh 3:

$Nilai \, dari\, \lim_{x\rightarrow \infty }\,\sqrt{4x^{2}-3x+1}-\sqrt{4x^{2}-2x+1}\, \, adalah.....$

Penyelesaian:

$\lim_{x\rightarrow \infty }\sqrt{4x^{2}-3x+1}-\sqrt{4x^{2}-2x+1}.\left (\frac{\sqrt{4x^{2}-3x+1}+\sqrt{4x^{2}-2x+1}}{\sqrt{4x^{2}-3x+1}+\sqrt{4x^{2}-3x+1}} \right )$

$\lim_{x\rightarrow \infty }\sqrt{4x^{2}-3x+1}-\sqrt{4x^{2}-2x+1}=\lim_{x\rightarrow \infty }\frac{\left ( 4x^{2}-3x+1)-\left ( 4x^{2}-2x+1 \right ) \right )}{\sqrt{4x^{2}-3x+1}+\sqrt{4x^{2}-2x+1}}$

$\lim_{x\rightarrow \infty }\sqrt{4x^{2}-3x+1}-\sqrt{4x^{2}-2x+1}=\lim_{x\rightarrow \infty }\frac{-x}{\sqrt{4x^{2}-3x+1}+\sqrt{4x^{2}-2x+1}}$

$\lim_{x\rightarrow \infty }\sqrt{4x^{2}-3x+1}-\sqrt{4x^{2}-2x+1}=\lim_{x\rightarrow \infty }\frac{\frac{-x}{x}}{\sqrt{\frac{4x^{2}}{x^{2}}-\frac{3x}{x^{2}}+\frac{1}{x^{2}}}+\sqrt{\frac{4x^{2}}{x^{2}}-\frac{2x}{x^{2}}+\frac{1}{x^{2}}}}$

Dengan menggunakan Teorema bahwa:

$\lim_{x\rightarrow \infty }\frac{a}{x^{n}}=0$

maka:

$\lim_{x\rightarrow \infty }\sqrt{4x^{2}-3x+1}-\sqrt{4x^{2}-2x+1}=\frac{-1}{\sqrt{4}+\sqrt{4}}$

$\lim_{x\rightarrow \infty }\sqrt{4x^{2}-3x+1}-\sqrt{4x^{2}-2x+1}=\frac{-1}{2+2}=\frac{-1}{4}$

Alternatif II:

$\lim_{x\rightarrow \infty }\sqrt{4x^{2}-3x+1}-\sqrt{4x^{2}-2x+1}=L$

$Jadi \, L=\frac{-3-(-2)}{2\sqrt{4}}=\frac{-1}{2.2}=\frac{-1}{4}$

Contoh 4:

$Nilai \, \lim_{x\rightarrow \infty }\sqrt{4x-3}\left ( \sqrt{4x-1}-\sqrt{4x+2} \right )=.........$

Penyelesaian:

$\lim_{x\rightarrow \infty }\sqrt{4x-3}\left ( \sqrt{4x-1}-\sqrt{4x+2} \right )=\lim_{x\rightarrow \infty }\, \sqrt{(4x-3)(4x-1)}-\sqrt{(4x-3)(4x+2)}$

$\lim_{x\rightarrow \infty }\sqrt{4x-3}\left ( \sqrt{4x-1}-\sqrt{4x+2} \right )=\lim_{x\rightarrow \infty }\, \sqrt{16x^{2}-16x+3}-\sqrt{16x^{2}-4x-6}$

Dengan menggunakan rumus ini:

$\blacksquare \, \, L=\frac{b-p}{2\sqrt{a}} ,untuk\, a=p$

maka diperoleh:

$\lim_{x\rightarrow \infty }\sqrt{4x-3}\left ( \sqrt{4x-1}-\sqrt{4x+2} \right )=\frac{-16-(-4)}{2\sqrt{16}}$

$\lim_{x\rightarrow \infty }\sqrt{4x-3}\left ( \sqrt{4x-1}-\sqrt{4x+2} \right )=\frac{-12}{2.4}$

$\lim_{x\rightarrow \infty }\sqrt{4x-3}\left ( \sqrt{4x-1}-\sqrt{4x+2} \right )=\frac{-3}{2}$

Contoh 5:

$Nilai \, dari\, \lim_{x\rightarrow \infty }\sqrt{5(x-1)+2\sqrt{4x^{2}-23x-6}}=...$

Penyelesaian:

$\lim_{x\rightarrow \infty }\sqrt{5(x-1)+2\sqrt{4x^{2}-23x-6}}=\lim_{x\rightarrow \infty }\, \sqrt{5(x-1)+2\sqrt{(4x+1)(x-6)}}$

Dengan mengingat konsep rumus bentuk akar:

$\sqrt{a+b+2\sqrt{ab}}=\sqrt{a}+\sqrt{b}$

$\lim_{x\rightarrow \infty }\sqrt{5(x-1)+2\sqrt{4x^{2}-23x-6}}=\lim_{x\rightarrow \infty }\, \sqrt{(4x+1)(x-6)+2\sqrt{(4x+1)(x-6)}}$

$\lim_{x\rightarrow \infty }\sqrt{5(x-1)+2\sqrt{4x^{2}-23x-6}}=\lim_{x\rightarrow \infty }\, \sqrt{4x+1}+\sqrt{x-6}$

$\lim_{x\rightarrow \infty }\sqrt{5(x-1)+2\sqrt{4x^{2}-23x-6}}=\infty$

Contoh 6:

$Nilai \, dari \, \lim_{x\rightarrow \infty }\, 4x\left ( \sqrt{16+\frac{10}{x}}-4 \right )=.....$

Penyelesaian:
$=\lim_{x\rightarrow \infty }\, 4x\left ( \sqrt{16+\frac{10}{x}}-4 \right ).\frac{\sqrt{16+\frac{10}{x}}+4}{\sqrt{16+\frac{10}{x}}+4}$

$=\lim_{x\rightarrow \infty }\, \frac{4x\left ( 16+\frac{10}{x}-16 \right )}{\sqrt{16+\frac{10}{x}}+4}$
$=\lim_{x\rightarrow \infty }\, \frac{40}{\sqrt{16+\frac{10}{x}}+4}$
$= \frac{40}{\sqrt{16+0}+4}$
$= \frac{40}{8}=5$

Contoh 7: (SIMAK UI)

$Nilai\, dari\, \lim_{x\rightarrow \infty }\, \left ( \sqrt{4x^{2}+12x+1} -\sqrt{x^{2}+x-1}-\sqrt{x^{2}-x+1}\right )=...$

Penyelesaian:

Untuk menentukan hasil dari limit di atas maka dapat digunakan dengan mengaklikan sekawan atau memanipulasi limit di atas sehingga sesuai dengan aturan yang berlaku yaitu:

$\lim_{x\rightarrow \infty }\sqrt{ax^{2}+bx+c}-\sqrt{px^{2}+qx+r}=L$

$\blacksquare \, \, L=0, untuk\, a=p$

$\lim_{x\rightarrow \infty }\, \left ( \sqrt{4x^{2}+12x+1} -\sqrt{x^{2}+x-1}-\sqrt{x^{2}-x+1}\right )$
diselesaikan dengan konsep:

$=\lim_{x\rightarrow \infty }\sqrt{4\left ( x^{2}+3x+\frac{1}{4} \right )}-\lim_{x\rightarrow \infty }\, \sqrt{x^{2}+X-1}-\lim_{X\rightarrow \infty }\, \sqrt{x^{2}-x+1}$
$=2\lim_{x\rightarrow \infty }\sqrt{x^{2}+3x+\frac{1}{4}}-\lim_{x\rightarrow \infty }\, \sqrt{x^{2}+x-1}-\lim_{x\rightarrow \infty }\, \sqrt{x^{2}-x+1}$

$=\lim_{x\rightarrow \infty }\sqrt{x^{2}+3x+\frac{1}{4}}-\lim_{x\rightarrow \infty }\sqrt{x^{2}+x-1}+\lim_{x\rightarrow \infty }\sqrt{x^{2}+3x+\frac{1}{4}}-\lim_{x\rightarrow \infty }\sqrt{x^{2}-x+1}$

$=\frac{3-1}{2\sqrt{1}}+\frac{3-(-1)}{2\sqrt{1}}$

$=3$

atau dapat diselesaikan secara langsung dengan cara cepat:

$Nilai\, dari\, \lim_{x\rightarrow \infty }\, \left ( \sqrt{4x^{2}+12x+1} -\sqrt{x^{2}+x-1}-\sqrt{x^{2}-x+1}\right )=...$

$L=\frac{12}{2\sqrt{4}}-\frac{1}{2\sqrt{1}}-\frac{(-1)}{2\sqrt{1}}$

$L=\frac{12}{2\sqrt{4}}-\frac{1}{2\sqrt{1}}-\frac{(-1)}{2\sqrt{1}}=3-\frac{1}{2}+\frac{1}{2}=3$

Contoh 8:

$Nilai\, dari\, \lim_{x\rightarrow \infty }\sqrt{x^{2}+3x-5}+\sqrt{x^{2}-x+2}-\sqrt{4x^{2}+8x-5}=....$

Penyelesaian:

$Hasil\, \lim_{x\rightarrow \infty }\sqrt{x^{2}+3x-5}+\sqrt{x^{2}-x+2}-\sqrt{4x^{2}+8x-5}\, dapat\, ditentukan:$

$L=\frac{3}{2\sqrt{1}}+\frac{-1}{2\sqrt{1}}-\frac{8}{2\sqrt{4}}$

$L=\frac{3}{2}-\frac{1}{2}-2$

$L=-1$

Contoh 9:

$Nilai \, \, dari\, \, \lim_{x\rightarrow \infty }\, \frac{3^{x+1}+2^{x}-3}{3^{x+2}-2^{x-1}+4}\, adalah.....$

Penyelesaian:
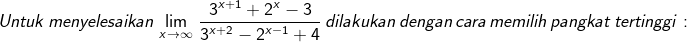
$Untuk\, menyelesaikan\, \lim_{x\rightarrow \infty }\, \frac{3^{x+1}+2^{x}-3}{3^{x+2}-2^{x-1}+4}\, dilakukan\, dengan\, cara\, memilih\, pangkat \, tertinggi:$

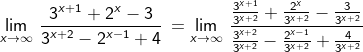
$\lim_{x\rightarrow \infty }\, \frac{3^{x+1}+2^{x}-3}{3^{x+2}-2^{x-1}+4}\,=\lim_{x\rightarrow \infty }\, \frac{\frac{3^{x+1}}{3^{x+2}}+\frac{2^{x}}{3^{x+2}}-\frac{3}{3^{x+2}}}{\frac{3^{x+2}}{3^{x+2}}-\frac{2^{x-1}}{3^{x+2}}+\frac{4}{3^{x+2}}}$

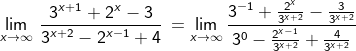
$\lim_{x\rightarrow \infty }\, \frac{3^{x+1}+2^{x}-3}{3^{x+2}-2^{x-1}+4}\,=\lim_{x\rightarrow \infty }\frac{3^{-1}+\frac{2^{x}}{3^{x+2}}-\frac{3}{3^{x+2}}}{3^{^{0}}-\frac{2^{x-1}}{3^{x+2}}+\frac{4}{3^{x+2}}}$

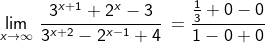
$\lim_{x\rightarrow \infty }\, \frac{3^{x+1}+2^{x}-3}{3^{x+2}-2^{x-1}+4}\,=\frac{\frac{1}{3}+0-0}{1-0+0}$

$\lim_{x\rightarrow \infty }\, \frac{3^{x+1}+2^{x}-3}{3^{x+2}-2^{x-1}+4}\,=\frac{1}{3}$

Contoh 10:

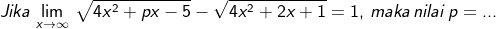
$Jika\, \lim_{x\rightarrow \infty }\,\sqrt{4x^{2}+px-5}-\sqrt{4x^{2}+2x+1}=1,\, maka\, nilai \, p=...$

Penyelesaian:

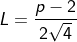
$\,L=\frac{p-2}{2\sqrt{4}}$

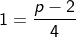
$\,1=\frac{p-2}{4}$

$\,4= p-2$

$p=6$

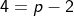
Contoh 10:

$Nilai\, dari\, \lim_{x\rightarrow \infty } \, \sqrt[3]{8^{x}+3^{x}}-\sqrt{4^{x}-2^{x}}\, adalah...$

Penyelesaian:

$\lim_{x\rightarrow \infty } \, \sqrt[3]{8^{x}+3^{x}}-\sqrt{4^{x}-2^{x}}\, =\lim_{x\rightarrow \infty }\sqrt[3]{8^{x}\left ( 1+\frac{3^{x}}{8^{x}} \right )}-\sqrt{4^{x}\left ( 1-\frac{2^{x}}{4^{x}} \right )}$

$\lim_{x\rightarrow \infty } \, \sqrt[3]{8^{x}+3^{x}}-\sqrt{4^{x}-2^{x}}\, =\lim_{x\rightarrow \infty }2^{x}.\sqrt[3]{1+\left ( \frac{3}{8} \right )^{x}}-2^{x}\sqrt{1-\left ( \frac{2}{4} \right )^{x}}$

$\lim_{x\rightarrow \infty } \, \sqrt[3]{8^{x}+3^{x}}-\sqrt{4^{x}-2^{x}}\, =\lim_{x\rightarrow \infty }2^{x}.\left ( \sqrt[3]{1+\left ( \frac{3}{8} \right )^{x}} -\sqrt{1-\left ( \frac{1}{2} \right )^{x}}\right )$

$\lim_{x\rightarrow \infty } \, \sqrt[3]{8^{x}+3^{x}}-\sqrt{4^{x}-2^{x}}\, =\lim_{x\rightarrow \infty }2^{x}.\lim_{x\rightarrow \infty }\left ( \sqrt[3]{1+\left ( \frac{3}{8} \right )^{x}} -\sqrt{1-\left ( \frac{1}{2} \right )^{x}}\right )$

Untuk menyelesaikan bentuk soal seperti ini, kita akan menggunakan Aproksimasi Binomial (Pendekatan Binomial) sehingga diperoleh:

$\lim_{x\rightarrow \infty } \left ( \sqrt[3]{1+\left ( \frac{3}{8} \right )^{x}}-\sqrt{1-\left ( \frac{1}{2} \right )^{x}} \right )=\lim_{x\rightarrow \infty }\left ( 1+\frac{1}{3}\left ( \frac{3}{8} \right )^{x}-\left ( 1-\frac{1}{2}\left ( \frac{1}{2} \right )^{x} \right ) \right )$

maka:

$\lim_{x\rightarrow \infty } \, \sqrt[3]{8^{x}+3^{x}}-\sqrt{4^{x}-2^{x}}\, =\lim_{x\rightarrow \infty }2^{x}.\lim_{x\rightarrow \infty }\left ( 1+\frac{1}{3}\left ( \frac{3}{8} \right )^{x}-\left ( 1-\frac{1}{2}\left ( \frac{1}{2} \right )^{x} \right ) \right )$

$\lim_{x\rightarrow \infty } \, \sqrt[3]{8^{x}+3^{x}}-\sqrt{4^{x}-2^{x}}\, =\lim_{x\rightarrow \infty }2^{x}.\lim_{x\rightarrow \infty }\left ( \frac{1}{3}\left ( \frac{3}{8} \right )^{x}+\left ( \frac{1}{2}\left ( \frac{1}{2} \right )^{x} \right ) \right )$

$\lim_{x\rightarrow \infty } \, \sqrt[3]{8^{x}+3^{x}}-\sqrt{4^{x}-2^{x}}\, =\lim_{x\rightarrow \infty }2^{x}.\left ( \frac{1}{3}\left ( \frac{3}{8} \right )^{x}+\left ( \frac{1}{2}\left ( \frac{1}{2} \right )^{x} \right ) \right )$

$\lim_{x\rightarrow \infty } \, \sqrt[3]{8^{x}+3^{x}}-\sqrt{4^{x}-2^{x}}\, =\lim_{x\rightarrow \infty }\left ( \frac{1}{3}\left ( \frac{6}{8} \right )^{x}+\left ( \frac{1}{2}\left ( \frac{2}{2} \right )^{x} \right ) \right )$

$\lim_{x\rightarrow \infty } \, \sqrt[3]{8^{x}+3^{x}}-\sqrt{4^{x}-2^{x}}\, =\frac{1}{3}(0)+\frac{1}{2}.(1)$

$\lim_{x\rightarrow \infty } \, \sqrt[3]{8^{x}+3^{x}}-\sqrt{4^{x}-2^{x}}\, =0+\frac{1}{2}$

$\lim_{x\rightarrow \infty } \, \sqrt[3]{8^{x}+3^{x}}-\sqrt{4^{x}-2^{x}}\, =\frac{1}{2}$

Baca Juga:

Contoh 11:

$Nilai\, dari\, \lim_{x\rightarrow \infty }\frac{\sqrt{4x^{2}-2x-6}\, -\, \sqrt{4x^{2}-8x+10}}{\sqrt{9x^{2}-3x-6}\, -\, \sqrt{9x^{2}+2x-3}}=....$

Penyelesaian:

$\lim_{x\rightarrow \infty }\frac{\sqrt{4x^{2}-2x-6}\, -\, \sqrt{4x^{2}-8x+10}}{\sqrt{9x^{2}-3x-6}\, -\, \sqrt{9x^{2}+2x-3}}=\frac{\frac{-2-(-8)}{2\sqrt{4}}}{\frac{-3-2}{2\sqrt{9}}}$

$\lim_{x\rightarrow \infty }\frac{\sqrt{4x^{2}-2x-6}\, -\, \sqrt{4x^{2}-8x+10}}{\sqrt{9x^{2}-3x-6}\, -\, \sqrt{9x^{2}+2x-3}}=\frac{\frac{6}{4}}{\frac{-5}{6}}$

$\lim_{x\rightarrow \infty }\frac{\sqrt{4x^{2}-2x-6}\, -\, \sqrt{4x^{2}-8x+10}}{\sqrt{9x^{2}-3x-6}\, -\, \sqrt{9x^{2}+2x-3}}=\frac{-36}{20}$

$\lim_{x\rightarrow \infty }\frac{\sqrt{4x^{2}-2x-6}\, -\, \sqrt{4x^{2}-8x+10}}{\sqrt{9x^{2}-3x-6}\, -\, \sqrt{9x^{2}+2x-3}}=\frac{-9}{5}$

Contoh 12:

$Nilai\, \, dari\, \, \lim_{x\rightarrow \infty }\frac{\sqrt{4x^{2}-2x-6}\, -\, \sqrt{4x^{2}-8x+10}}{\sqrt[3]{8x^{3}-2x^{2}+x-6}-\sqrt[3]{8x^{3}-6x+10x-3}}=.....$

Penyelesaian:

$\lim_{x\rightarrow \infty }\frac{\sqrt{4x^{2}-2x-6}\, -\, \sqrt{4x^{2}-8x+10}}{\sqrt[3]{8x^{3}-2x^{2}+x-6}-\sqrt[3]{8x^{3}-6x+10x-3}}=\frac{\frac{-2-(-8)}{2\sqrt{4}}}{\frac{-2-(-6)}{3\sqrt[3]{8^{2}}}}$

$\lim_{x\rightarrow \infty }\frac{\sqrt{4x^{2}-2x-6}\, -\, \sqrt{4x^{2}-8x+10}}{\sqrt[3]{8x^{3}-2x^{2}+x-6}-\sqrt[3]{8x^{3}-6x+10x-3}}=\frac{\frac{6}{4}}{\frac{4}{12}}$

$\lim_{x\rightarrow \infty }\frac{\sqrt{4x^{2}-2x-6}\, -\, \sqrt{4x^{2}-8x+10}}{\sqrt[3]{8x^{3}-2x^{2}+x-6}-\sqrt[3]{8x^{3}-6x+10x-3}}=\frac{72}{16}$

$\lim_{x\rightarrow \infty }\frac{\sqrt{4x^{2}-2x-6}\, -\, \sqrt{4x^{2}-8x+10}}{\sqrt[3]{8x^{3}-2x^{2}+x-6}-\sqrt[3]{8x^{3}-6x+10x-3}}=\frac{9}{2}$

Contoh 13:

$Nilai\, dari \, \lim_{x\rightarrow \infty }\frac{\sqrt[3]{27x^{3}+3x^{2}-2x-6}\, -\, \sqrt[3]{27x^{3}-8x+10}}{\sqrt[3]{8x^{3}-2x^{2}+x-6}-\sqrt[3]{8x^{3}-6x+10x-3}}=.....$

Penyelesaian:

$\lim_{x\rightarrow \infty }\frac{\sqrt[3]{27x^{3}+3x^{2}-2x-6}\, -\, \sqrt[3]{27x^{3}-8x+10}}{\sqrt[3]{8x^{3}-2x^{2}+x-6}-\sqrt[3]{8x^{3}-6x+10x-3}}=\frac{\frac{3-0}{3\sqrt[3]{27^{2}}}}{\frac{-2-(-6)}{3\sqrt[3]{8^{2}}}}$

$\lim_{x\rightarrow \infty }\frac{\sqrt[3]{27x^{3}+3x^{2}-2x-6}\, -\, \sqrt[3]{27x^{3}-8x+10}}{\sqrt[3]{8x^{3}-2x^{2}+x-6}-\sqrt[3]{8x^{3}-6x+10x-3}}=\frac{\frac{3}{27}}{\frac{4}{12}}$

$\lim_{x\rightarrow \infty }\frac{\sqrt[3]{27x^{3}+3x^{2}-2x-6}\, -\, \sqrt[3]{27x^{3}-8x+10}}{\sqrt[3]{8x^{3}-2x^{2}+x-6}-\sqrt[3]{8x^{3}-6x+10x-3}}=\frac{\frac{1}{9}}{\frac{1}{3}}$

$\lim_{x\rightarrow \infty }\frac{\sqrt[3]{27x^{3}+3x^{2}-2x-6}\, -\, \sqrt[3]{27x^{3}-8x+10}}{\sqrt[3]{8x^{3}-2x^{2}+x-6}-\sqrt[3]{8x^{3}-6x+10x-3}}=\frac{1}{3}$