Materi, Soal dan Pembahasan Olimpiade Ketidaksamaan QM-AM-GM-HM

Salam Para Bintang

Kali ini saya akan coba berbagi tentang salah satu materi Olimpiade yang sangat sering muncul. Dalam dunia sekolah, materi ini sangat jarang terdengar bagi siswa/i yang tidak fokus ke Olimpiade. Soal ini hanya banyak digunakan ketika berhadapan dalam soal Olimpade mulai dari KSK,KSP, dan KSN maupun tingkat internasional.

Tetapi tidak ada salahnya kita bahas dan pelajari secara dalam dari sekarang, untuk mempersiapkan diri kita masuk ke dalam dunia olimpiade. Untuk memahami materi ketaksamaan QM-AM-GM-HM, langsung kita bahas satu per satu. Simak secar mendalam !

1. Rataan Kuadrat (Quadrat Mean-QM)

Jika diberikan data (bilangan) $x_{1},x_{2},x_{3},......,x_{n}$ , maka nilai dari rataan kuadrat data tersebut dapat dirumuskan dengan:

$QM=\sqrt{\frac{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+......+x_{n}^{2}}{n}}$

untuk data a dan b maka:

$QM=\sqrt{\frac{a^{2}+b^{2}}{2}}$

untuk data a,b dan c maka:

$QM=\sqrt{\frac{a^{2}+b^{2}+c^{2}}{3}}$

2. Rataan Aritmetik (Arithmetic Mean-AM)

Jika diberikan data (bilangan) $x_{1},x_{2},x_{3},......,x_{n}$ , maka nilai dari rataan aritmetik data tersebut dapat dirumuskan dengan:

$AM=\frac{x_{1}+x_{2}+x_{3}+.......+x_{n}}{n}$

Untuk data a, b maka:

$AM=\frac{a+b}{2}$

Untuk data a, b dan c maka:

$AM=\frac{a+b+c}{3}$

3. Rataan Gemetrik (Geometric Mean- GM)

Jika diberikan data (bilangan) $x_{1},x_{2},x_{3},......,x_{n}$ , maka nilai dari rataan geometrik data tersebut dapat dirumuskan dengan:

$GM=\sqrt[n]{x_{1}.x_{2}.x_{3}.......x_{n}}$

untuk data a,b maka:

$GM=\sqrt{ab}$

untuk data a,b dan c maka:

$GM=\sqrt[3]{abc}$

4. Rataan Harmonik (Harmonic Mean -HM)

Jika diberikan data (bilangan) $x_{1},x_{2},x_{3},......,x_{n}$ , maka nilai dari rataan harmonik data tersebut dapat dirumuskan dengan:

$HM=\frac{n}{\frac{1}{x_{1}}+\frac{1}{x_{2}}+\frac{1}{x_{3}}+..........+\frac{1}{x_{n}}}$

Untuk data a, b maka:

$HM=\frac{2ab}{a+b}$

Untuk data a, b dan c maka:

$HM=\frac{3abc}{ab+bc+ac}$

Nah, kesimpulan yang dapat kita tarik adalah bahwa:

Untuk data yang sudah terurut dari terkecil ke yang terbesar diperoleh hubungan QM-AM-GM-HM yaitu:

$x_{min}\leq HM\leqslant GM\leqslant AM\leqslant QM\leqslant x_{maks}$ atau,

$x_{maks}\geqslant QM\geqslant AM\geqslant GM\geqslant HM\geq x_{min}$

maka untuk data a,b diperoleh hubungan:

$\frac{2ab}{a+b}\leqslant \sqrt{ab}\leqslant \frac{a+b}{2}\leqslant \sqrt{\frac{a^{2}+b^{2}}{2}}$

Untuk mempertajam penguasaan kita terhadaap materi ini, diperlukan pembahasan soal dan berlatih soal-soal yang menggunaka konsep ini. Sekarang mari kita simak soalnya satu persatu:

Contoh 1:

Nilai minimum dari :

$f(x)=\frac{9x^{2}\, \, sin^{2}x+4}{x\, sin\, x}$

untuk $0<x<\pi$ adalah.......

Pembahasan:

Dengan menyerderhanakan:

$f(x)=\frac{9x^{2}\, \, sin^{2}x+4}{x\, sin\, x}\, \, menjadi:f(x)=9x\, sin\, x+\frac{4}{x\, sin\, x}$

Dengan menggunakan ketaksamaan AM-GM, maka diperoleh:

$AM\geqslant GM$

$9x\, sin\, x+\frac{4}{x\, sin\, x}\geqslant2\sqrt{9x\, sin\, x\left ( \frac{4}{x\, sin\, x} \right )}$

$9x\, sin\, x+\frac{4}{x\, sin\, x}\geqslant2\sqrt{36}$

$9x\, sin\, x+\frac{4}{x\, sin\, x}\geqslant 12$

Dari penyelesaian di atas diperoleh bahwa nilai minimum f(x) adalah 12

Contoh 2:

Banyaknya pasangan bilangan real (a,b) yang memenuhi persamaan $a^{4}+b^{4}=4ab-2$ adalah....

Pembahasan:

$a^{4}+b^{4}=4ab-2\approx a^{4}+b^{4}+2=4ab$

Dengan menggunakan ketaksamaan AM-GM, maka diperoleh:

$AM\geqslant GM$

$a^{4}+b^{4}\geq 2\sqrt{a^{4}.b^{4}}$

$a^{4}+b^{4}\geq 2\left ( ab \right )^{2}$

$a^{4}+b^{4}+2\geq 2\left ( ab \right )^{2}+2$

Karena $a^{4}+b^{4}+2=4ab$ , maka diperoleh:

$2\left ( ab \right )^{2}+2=4ab$

$2\left ( ab \right )^{2}-4(ab)+2=0$

$\left ( ab \right )^{2}-2(ab)+1=0$

$(ab-1)^{2}=0\, \, maka:ab=1$

maka:

$a^{4}+b^{4}=4ab-2\rightarrow a^{4}+b^{4}=4(1)-2=2$

Kesamaan dapat terjadi apabila

$a^{4}=b^{4}\rightarrow a^{4}+b^{4}=2b^{4}=2$

maka

$b=\pm 1\, \, dan\, a=\pm 1,\, \, karena\, ab=1\, \, maka\, \, a\, \, dan\, b\, \,$ harus bertanda sama.

Sehingga diperoleh, banyak pasangan real (a,b) yang memenuhi adalah 2 yaitu (1,1) dan (-1,-1)

Contoh 3:

Untuk bilangan real positif x

x

dan

y

dengan $xy=\frac{1}{3}$ . Tentukan nilai minimum dari $\frac{1}{9x^{6}}+\frac{1}{4y^{6}}\, \, adalah.....$

x y = \frac{1}{3}

Pembahasan:

Dengan menggunakan ketaksamaan AM-GM, maka diperoleh:

$AM\geqslant GM$

$\frac{1}{9x^{6}}+\frac{1}{4y^{6}}\, \,\geqslant 2\sqrt{\frac{1}{9x^{6}}.\frac{1}{4y^{6}}}$
$\frac{1}{9x^{6}}+\frac{1}{4y^{6}}\, \,\geqslant 2\sqrt{\frac{1}{36(xy)^{6}}}$
$\frac{1}{9x^{6}}+\frac{1}{4y^{6}}\, \,\geqslant2.\frac{1}{6\left ( xy \right )^{3}}$
$\frac{1}{9x^{6}}+\frac{1}{4y^{6}}\, \,\geqslant.\frac{1}{3\left ( xy \right )^{3}}$

Karena diketahui bahwa $xy=\frac{1}{3}$ , maka:

$\frac{1}{9x^{6}}+\frac{1}{4y^{6}}\, \,\geqslant.\frac{1}{3\left ( \frac{1}{3} \right )^{3}}$
$\frac{1}{9x^{6}}+\frac{1}{4y^{6}}\, \,\geqslant\frac{1}{\frac{1}{9}}$
$\frac{1}{9x^{6}}+\frac{1}{4y^{6}}\, \,\geqslant9$

Jadi, nilai minimumnya adalah 9

Contoh 4:

Nilai minimum dari $x+\frac{1}{x^{2}}$ dalah.....

Pembahasan:

Dengan memanipulasi $x+\frac{1}{x^{2}}$ menjadi

$f(x)=x+\frac{1}{x^{2}}=\frac{x}{2}+\frac{x}{2}+\frac{1}{x^{2}}$

Dengan menggunakan ketaksamaan AM-GM, menggunakan 3 suku maka diperoleh:

$AM\geqslant GM$

$\frac{x}{2}+\frac{x}{2}+\frac{1}{x^{2}}\geqslant 3\, \, \sqrt[3]{\frac{x}{2}.\frac{x}{2}.\frac{1}{x^{2}}}$

$\frac{x}{2}+\frac{x}{2}+\frac{1}{x^{2}}\geqslant 3\, \, \sqrt[3]{\frac{1}{4}}$

Nilai minimumnya adalah $3\sqrt[3]{\frac{1}{4}}$

Contoh 5:

Diberikan

f (x) = x^{2} + 4

. Misalkan

x

dan

y

adalah bilangan-bilangan real positif yang memenuhi

f (x y) + f (y - x) = f (y + x)

. Nilai minimum dari

x + y

adalah...

Pembahasan:

Dengan menentukan f(xy), f(y-x) dan f(y+x) yaitu:

$\blacksquare f(xy)=(xy)^{2}+4=x^{2}y^{2}+4$
$\blacksquare f(y-x)=(y-x)^{2}+4=y^{2}-2xy+x^{2}+4$
$\blacksquare f(y+x)=(y+x)^{2}+4=y^{2}+2xy+x^{2}+4$

sehingga diperoleh:

$x^{2}y^{2}+4+y^{2}-2yx+x^{2}+4=y^{2}+2xy+x^{2}+4$

x2y2−4xy+4=0(xy−2)=0xy−2=0xy=2

Dengan menggunakan ketaksamaan AM-GM, menggunakan 2 suku maka diperoleh:

$AM\geqslant GM$

$x+y\geq 2\sqrt{xy}$

Karena xy = 2,maka

$x+y\geq 2\sqrt{2}$

Jadi, nilai minimumnya adalah $2\sqrt{2}$

Contoh 6:

Jika jumlah dua bilangan bulat positif adalah 24, maka nilai terkecil dari jumlah kebalikan bilangan-bilangan tersebut adalah....

Pembahasan:

Misalkan bilangan bulat positif tersebut adalah x dan y, sehingga x + y = 24. Pertanyaannya adalah nilai maksimum kebalikan bilangan tersebut yaitu 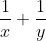$\frac{1}{x}+\frac{1}{y}$ .

Dengan menggunakan ketaksamaan AM-HM, menggunakan 2 suku maka diperoleh:

$AM\geqslant HM$
$\frac{x+y}{2 }\geqslant \frac{2}{\frac{1}{x}+\frac{1}{y}}$
$\frac{24}{2 }\geqslant \frac{2}{\frac{1}{x}+\frac{1}{y}}$

$12\geqslant \frac{2}{\frac{1}{x}+\frac{1}{y}}$
$\frac{1}{x}+\frac{1}{y}\geqslant \frac{1}{6}$

Jadi,nilai minimum jumlah kebalikan bilangan-bilangan tersebut adalah $\frac{1}{6}$

Contoh 7:

Banyaknya bilangan real x yang memenuhi persamaan

$x^{4}-2x^{3}+5x^{2}-176x+2009=0$ adalah...

Pembahasan:

Dengan menggunakan ketaksamaan AM-GM, menggunakan 5 suku maka diperoleh:

$AM\geqslant GM$

$\frac{x^{4}-2x^{3}+5x^{2}-176x+2009}{5}\geqslant \sqrt[5]{\left ( x^{4} \right ).\left ( 2x^{3} \right ).\left ( 5x^{2} \right ).\left ( -176x \right ).\left ( 2009 \right )}$
$\frac{0}{5}\geqslant \sqrt[5]{\left ( x^{4} \right ).\left ( 2x^{3} \right ).\left ( 5x^{2} \right ).\left ( -176x \right ).\left ( 2009 \right )}$

$\frac{0}{5}\geqslant \sqrt[5]{\left ( 1760.2009.x^{10} \right )}$
$0\geqslant 1760.2009.x^{10}$

Ketaksamaan di atas bernilai benar apabila 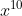$x^{10}$ bernilai negatif atau nol. Karena x adalah bilangan real sudah dipastikan x tidaklah negatif yang artinya 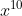$x^{10}$ adalah bernilai 0. Jika disubsitusi x = 0 ke persamaan 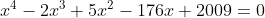$x^{4}-2x^{3}+5x^{2}-176x+2009=0$ , maka tidak akan ditemukan hasilnya 2009 (bukan nol).

Jadi, diperoleh tidakada satupun bilangan real x yang memenuhi $x^{4}-2x^{3}+5x^{2}-176x+2009=0$