Materi Terlengkap, Contoh Soal + Contoh Persamaan Garis Singgung Lingkaran

Salam Para Bintang

Garis singgung lingkaran adalah garis yang memotong lingkaran tepat pada satu titik dan titik tersebut. Ada 3 jenis cara menentukan persamaan garis singgung lingkaran yaitu jika diketahui:

Garis singgung melalui suatu titik pada lingkaran
Garis singgung melalui suatu titik di luar lingkaran
Garis singgung lingkaran jika diketahui gradien garisnya

Sebelum kita membahas topik ini perlu kalian pahami materi tentang persamaan lingkaran yaitu

1. Persamaan Garis Singgung Lingkaran melalui suatu titik pada lingkaran

Persamaan garis singgung lingkaran melalui titik pada lingkaran harus dipahami bahwa titik yang dilalui garis terdapat pada lingkaran tersebut. Persamaan garis singgung lingkaran melalui suatu titik pada lingkaran tergantung pusat lingkaran tersebut yaitu sebagai berikut:

a. Persamaan Garis singgung lingkaran pusat O(0,0) pada titik $A(x_{1},y_{1})$

Perhatikan gambar berikut:

Persamaan garis singgungnya adalah:

$x_{1}x+y_{1}y=r^{2}$

Contoh 1:

Pembahasan:

Pertama kita melakukan uji coba, apakah titik(2,-3) terletak pada lingkaran 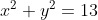$x^{2}+y^{2}=13$ , dengan melakukan subsitusi:

$2^{2}+(-3)^{2}=13$

$4+9=13$

$13=13 (terbukti)$

Karena titik (2,-3) terletak pada lingkaran $x^{2}+y^{2}=13$ , maka diperoleh persamaan garis singgungnya adalah:

$x_{1}x+y_{1}y=r^{2}$

$2x-3y=13$

b. Persamaan Garis singgung lingkaran pusat A(p,q) pada titik $M(x_{1},y_{1})$

Perhatikan gambar berikut:

Persamaan garis singgungnya adalah:

$(x_{1}-p)(x-p)+(y_{1}-q)(y-q)=r^{2}$

Contoh 2:

Persamaan garis singgung lingkaran melalui titik (3,1) pada lingkaran . $(x-1)^{2}+(y-4)^{2}=25$ dan titik singung A(-3,1) .

Pembahasan:

$(-3-1)^{2}+(1-4)^{2}=25$

$16+9=25$

$25=25 (terbukti)$

Karena titik (-3,1) terletak pada lingkaran $(x-1)^{2}+(y-4)^{2}=25$ , maka diperoleh persamaan garis singgungnya adalah:

$(x_{1}-p)(x-p)+(y_{1}-q)(y-q)=r^{2}$

$(-3-1)(x-1)+(1-4)(y-4)=25$

$-4(x-1)-3(y-4)=25$

$-4x+4-3y+12=25$

$4x+3y + 9 = 0$

c. Persamaan Garis singgung lingkaran $x^{2}+y^{2}+Ax+By+C=0$ pada titik $M(x_{1},y_{1})$

Persamaan garis singgungnya adalah:

$x_{1}x+y_{1}y+\frac{1}{2}A(x+x_{1})+\frac{1}{2}B( y+y_{1})+C=0$

Contoh 3:

Persamaan garis singgung melalui titik (2, 1) pada lingkaran $L\equiv x^{2}+y^{2}-2x+4y-5=0$

Pembahasan:

Pertama kita melakukan uji coba, apakah titik(2,1) terletak pada lingkaran 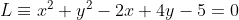$L\equiv x^{2}+y^{2}-2x+4y-5=0$ , dengan melakukan subsitusi:

$L\equiv x^{2}+y^{2}-2x+4y-5=0$

$2^{2}+1^{2}-2.2+4.1-5=0$

$0=0\, \, (terbukti)$

Karena titik (2,1) terletak pada lingkaran $L\equiv x^{2}+y^{2}-2x+4y-5=0$ , maka diperoleh persamaan garis singgungnya adalah:

$x_{1}x+y_{1}y+\frac{1}{2}A(x+x_{1})+\frac{1}{2}B( y+y_{1})+C=0$

$2x+y-\frac{1}{2}.2.(x+2)+\frac{1}{2}.4(y+1)+5=0$

$2x+y-(x+2)+2(y+1)+5=0$

$2x+y-x-2+2y+2+5=0$

$x+3y+5=0$

Persamaan garis singgung lingkaran melalui titik di luar lingkaran dapat dilihat bahwa ada sebuah titik di luar lingkaran, kemudian ditarik ke 2 titik pada lingkaran sehingga diperoleh garis menyinggung lingkaran. Perhatikan gambar berikut!

Dalam menentukan persamaan garis singgung lingkaran terdapat 2 cara,yaitu:

1. Persamaan Garis Singgung melalui titik $A(x_{1},y_{1})\,$ di luar lingkaran.

Cara menentukan persamaan garis singgung:

Misalkan garis singgungnya y = mx + n
Subsitusi titik $A(x_{1},y_{1})\,$ ke y = mx + n dan diperoleh nilai n
Subsitusi nilai n ke garis y = mx + n
Subsitusi garis yang baru diperoleh tersebut (dimana n sudah diganti) ke persamaan Lingkaran dengan menentukan nilai Diskriminan (D) yaitu D = 0
Dengan diperoleh nilai m, maka subsitusi nilai m ke garis yang baru tersebut kembali.

Contoh 4:

Carilah persamaan garis singgung pada lingkaran $x^{2}+y^{2}=25$ yang dapat ditarik dari titik (7, –1).

Pembahasan:

Persamaan garis singgung yang melalui (7, –1) dengan gradien m adalah :

y + 1 = m(x – 7)

y = mx – 7m – 1 ... (1)

Substitusi (1) ke persamaan lingkaran $x^{2}+y^{2}=25$ , diperoleh :

$x^{2}+(mx-7m-1)^{2}=25$

$x^{2}+\left ( (mx-7m)-1 \right )^{2}=25$

$x^{2}+\left ( mx-7m \right )^{2}-2(mx-7m)+1=25$ $x^{2}+m^{2}x^{2}-14m^{2}x+49m^{2}-2mx+14m+1=25$ $\left ( 1+m^{2} \right )x^{2}-(14m^{2}+2m)x+49m^{2}+14m-24=0$

Kemudian dicari nilai Diskriminan, yaitu:

$D=b^{2}-4.a.c$

Dari bentuk persamaan kuadrat di atas, diperoleh :

$a=1+m^{2};\, \, \, b= -(14m^{2}+2m);\, \, \, c=49m^{2}+14m-24$

maka:

$D=\left ( -(14m^{2}+2m) \right )^{2}-4.(1+m^{2})(49m^{2}+14m-24)$

$D=196m^{4}+56m^{3}+4m^{2}-4(49m^{2}+14m-24+49m^{4}+14m^{3}-24m^{2})$

$D= -96m^{2}-56m+96$

Ingat, syarat garis menyinggung lingkaran adalah D = 0, maka:

$-96m^{2}-56m+96=0$

$96m^{2}+56m-96=0$

$12m^{2}+7m-12=0\, \, (kedua \, \, ruas \, \, dibagi\, \, dengan\, \, 8)$

$(3m+4)(4m-3)=0$

$m=-\frac{4}{3}\, \, dan\, \, m=\, \frac{3}{4}$

Kemudian, subsitusi nilai $m=-\frac{4}{3}\, \, dan\, \, m=\, \frac{3}{4}$ , ke persamaan garis y = mx – 7m – 1. Sehingga diperoleh:

a. Persamaan Garis Singgung dengan gradien $m=-\frac{4}{3}$ , yaitu:

$y=-\frac{4}{3}x-7\left ( -\frac{4}{3} \right )-1$

$y=-\frac{4}{3}x+\frac{28}{3}-1$

$3y=-4x+28-3$

$4x+3y=25$

b. Persamaan Garis Singgung dengan gradien $m=\frac{3}{4}$ , yaitu:

$y=\frac{3}{4}x-7\left ( \frac{3}{4} \right )-1$

$y=\frac{3}{4}x-\frac{21}{4}-1$

$4y=3x-21-4$

$3x-4y=25$

2. Menggunakan garis polar (Garis Kutub)

Perhatikan gambar berikut !

Jika melalui titik $A(x_{1},y_{1})\,$ di luar lingkaran ditarik 2 buah garis pada lingkaran dengan titik singgungnya $B(x_{2},y_{2})\, \, dan\, \, C(x_{3},y_{3})$ , maka diperoleh persamaan garis polar BC yaitu:

a. $x_{1}x+y_{1}y=r^{2}$

b. $(x_{1}-p)(x-p)+(y_{1}-q)(y-q)=r^{2}$

Cara membuat persamaan garis singgung lingkaran:

Membuat persamaan garis polar dari titik $A(x_{1},y_{1})\,$ terhadap lingkaran.
Subsitusi persamaan garis polar ke persamaan lingkaran, dengan mencari nilai x
Subsitusi nilai x atau y ke persamaan garis polar, untuk menentukan titik B dan titik C

Persamaan garis polar yang ditarik dari titik A(2,2) terhadap lingkaran $(x+3)^{2}+(y-1)^{2}=16$ adalah.....

Pembahasan:

Pertama, menentukan garis polar yaitu ditarik dari titik A(2,2) dengan pusat lingkaran (-3,1) dan jari-jari r = 4 dengan menggunakan rumus:

$(x_{1}-p)(x-p)+(y_{1}-q)(y-q)=r^{2}$

maka:

$(2+3)(x+3)+(2-1)(y-1)=16$

$5(x+3)+y-1=16$

$5x+15+y-1-16=0$

$5x+y-2=0$

jadi, persamaan garis polarnya adalah $y=2-5x$

Kemudian, subsitusi $y=2-5x$ ke persamaan lingkaran $(x+3)^{2}+(y-1)^{2}=16$ :

$(x+3)^{2}+(y-1)^{2}=16$

$(x+3)^{2}+(2-5x-1)^{2}=16$

$(x+3)^{2}+(1-5x)^{2}=16$

$x^{2}+6x+9+1-10x+25x^{2}=16$

$26x^{2}-4x-6=0$

$13x^{2}-2x-3=0$

Dengan menggunakan rumus abc, maka dapat diperoleh nilai x yaitu:

$x_{1,2}=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

a = 13 , b = -2 dan c = -3

$x_{1,2}=\frac{-(-2)\pm \sqrt{(-2)^{2}-4(13)(-3)}}{2(13)}$

$x_{1,2}=\frac{2\pm \sqrt{4+156}}{26}$

$x_{1,2}=\frac{2\pm \sqrt{160}}{26}$

$x_{1,2}=\frac{2\pm 4\sqrt{10}}{26}$

$x_{1,2}=\frac{1\pm 2\sqrt{10}}{13}$

Jika $x_{1}=\frac{1+2\sqrt{10}}{13}$ maka diperoleh nilai $y=2-5x$ :

$y=2-5\left ( \frac{1+2\sqrt{10}}{13} \right )$

$y=\frac{26-5-10\sqrt{10}}{13}$

$y=\frac{21-10\sqrt{10}}{13}$

Jadi, titik singgungnya adalah $\left ( \frac{1+2\sqrt{10}}{13},\frac{21-10\sqrt{10}}{13} \right )$

Jika $x_{2}=\frac{1-2\sqrt{10}}{13}$ maka diperoleh $y=2-5x$ :

$y=2-5\left ( \frac{1-2\sqrt{10}}{13} \right )$

$y=\frac{26-5+10\sqrt{10}}{13}$

$y=\frac{21+10\sqrt{10}}{13}$

Jadi, titik singgungnya adalah $\left ( \frac{1-2\sqrt{10}}{13},\frac{21+10\sqrt{10}}{13} \right )$

3. Persamaan Garis Singgung Lingkaran melalui suatu titik di luar lingkaran

Persamaan garis singgung lingkaran dengan gradien m dapat dinyatakan dalam 3 bentuk yaitu berdasarkan persamaan lingkarannya :

Persamaan garis singgung lingkaran dengan gradien m terhadap lingkaran

$x^{2}+y^{2}=r^{2}$ .

Persamaan garis singgungnya adalah:

$y=mx\pm r\sqrt{m^{2}+1}$

Persamaan garis singgung lingkaran dengan gradien m terhadap lingkaran $\left ( x-p \right )^{2}+\left ( y-q \right )^{2}=r^{2}$

Persamaan garis singgungnya adalah:

$y-q=m(x-p)\pm r\sqrt{m^{2}+1}$

Persamaan garis singgung lingkaran dengan gradien m terhadap lingkaran

$x^{2}+y^{2}+Ax+By+C=0$

Persamaan garis singgungya adalah:

$y-q=m(x-p)\pm r\sqrt{m^{2}+1}$

Untuk menentukan niai p, q beserta jari-jari lingkaran dengan persamaan di atas, silahkan baca materi ini:

Baca Juga:

Persamaan Lingkaran dengan pusat A(p,q),cara menetukan pusat dan jari-jari !

Dalam materi persamaan garis singgung lingkaran dengan diketahi gradien sering sekali ditemukan hubungan antara 2 garis yaitu sejajar dan tegak lurus, maka:

Dua buah garis sejajar maka gradiennya adalah sama : $m_{1}=m_{2}$
Dua buah garis yang saling tegak lurus perkalian kedua gradiennya adalah -1 : $m_{1}.m_{2}=-1\, \, atau\, \, m_{2}=\frac{1}{m_{1}}$

Contoh 6:

Persamaan garis singgung lingkaran dengan gradien 2 pada lingkaran $x^{2}+y^{2}=5$ adalah.....

Pembahasan:

Diketahui dan diperoleh bahwa m = 2 dan 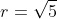$r=\sqrt{5}$ sehingga persamaan garis singgung lingkaran dengan gradien 2 dan 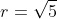$r=\sqrt{5}$ adalah:

$y=mx\pm r\sqrt{m^{2}+1}$

$y=2x\pm \sqrt{5}.\sqrt{2^{2}+1}$

$y=2x\pm 5$

Contoh 7:

Persamaan garis singgung lingkaran dengan gradien 2 pada lingkaran $\left ( x-2 \right )^{2}+\left ( y+1 \right )^{2}=1$ adalah.....

Pembahasan:

Diketahui dan diperoleh bahwa m = 2 dan r = 1 sehingga persamaan garis singgung lingkaran dengan gradien 2 dan r = 1 adalah:

$\left ( x-2 \right )^{2}+\left ( y+1 \right )^{2}=1$

$y-q=m(x-p)\pm r\sqrt{m^{2}+1}$

$y+1=2(x-2)\pm 1.\sqrt{1^{2}+1}$

$y+1=2x-4\pm \sqrt{2}$

$y=2x-5\pm \sqrt{2}$

Jadi, persamaan garis singgungnya adalah $y=2x-5+ \sqrt{2}$ dan $y=2x-5- \sqrt{2}$

Contoh 8:

Persamaan garis singgung lingkaran $x^{2}+y^{2}-12x+8y-48=0$ yang sejajar dengan x - 2y - 5 = 0 adalah.....

Pembahasan:

Diketahui persamaan lingkaran $x^{2}+y^{2}-12x+8y-48=0$ dan diperoleh:

Pusat lingkaran yaitu (6,-4) dan jari-jari adalah:

$r=\sqrt{\frac{1}{4}(-12)^{2}+\frac{1}{4}(8)^{2}-(-48)}$

$r=\sqrt{36+16+48}$

$r=\sqrt{100}$

$r=10$

Dengan menentukan gradien garis singgungnya dimana sejajar dengan garis x-2y -5 = 0, sehingga diperoleh gradiennya adalah :

$m=\frac{1}{2}$

Sehingga diperoleh persamaan garis singgung dengan rumus:

$y-q=m(x-p)\pm r\sqrt{m^{2}+1}$

$y+4=\frac{1}{2}(x-6)\pm 10\sqrt{\left ( \frac{1}{2} \right )^{2}+1}$

$y+4=\frac{1}{2}(x-6)\pm 10\sqrt{\left ( \frac{5}{4} \right )}$

$y+4=\frac{1}{2}(x-6)\pm 5\sqrt{5}$

$2y+8=x-6\pm 10\sqrt{5}$

$x-2y-14\pm 10\sqrt{5}$

Jadi, persamaan garis singgungnya adalah $x-2y-14\pm 10\sqrt{5}$

Contoh 9:

Persamaan garis singgung lingkaran $x^{2}+y^{2}=25$ yang tegak lurus dengan 2y-x + 3 = 0 adalah.....

Pembahasan:

Diketahui persamaan lingkaran $x^{2}+y^{2}=25$ dan diperoleh:

Pusat lingkaran yaitu (0,0) dan jari-jari adalah 5

Dengan menentukan gradien garis singgungnya dimana tegak lurus dengan garis 2y - x + 3 = 0, sehingga diperoleh gradiennya adalah :

$m=\frac{1}{2}$

karena : $m_{1}.m_{2}=-1$ maka:

$m_{2}=-\frac{1}{\frac{1}{2}}$

$m_{2}=2$

Sehingga diperoleh persamaan garis singgung dengan rumus:

$y=2x\pm 5\sqrt{2^{2}+1}$ $y=2x\pm 5\sqrt{5}$

Social Widget

Menu

Materi Terlengkap, Contoh Soal + Contoh Persamaan Garis Singgung Lingkaran

0 Comments

Materi, Soal dan Pembahasan Materi Kaidah Pencacahan: Permutasi

Materi, Contoh Soal dan Pembahasan Kaidah Pencacahan: Aturan Penjumlahan dan Aturan Perkalian

Materi,Contoh Soal dan Pembahasan tentang Faktorial + Soal-soal PTN

Materi Super Lengkap Matriks beserta Contoh Soal (UTBK SBMPTN, SIMAK UI,UGM)

Berita Terbaru: Jadwal dan Syarat Pendaftaran SNMPTN, UTBK, SBMPTN 2021

PENGERTIAN BILANGAN PALINDROME, BILANGAN TERUNIK DAN SIMETRI MUNCUL DI SOAL UTBK, WAJIB PAHAM !!

Soal, Materi Limit Trigonometri di Tak Hingga Mirip Soal UTBK SBMPTN

10 Aplikasi Belajar Terbaik Berbasis Game Menarik Bagi Siswa, Penyemangat Belajar Dari Rumah !!

Kumpulan Soal , Kunci dan Pembahasan Soal SCE USU IOSTPI 2019

Rumus-rumus Trigonometri: Rumus Perkalian Sinus dan Kosinus

Iklan

Materi, Soal dan Pembahasan Materi Kaidah Pencacahan: Permutasi

Materi, Contoh Soal dan Pembahasan Kaidah Pencacahan: Aturan Penjumlahan dan Aturan Perkalian

Materi,Contoh Soal dan Pembahasan tentang Faktorial + Soal-soal PTN