Salam Para Bintang
Kali ini kita melanjutkan materi berikutnya yaitu tentang Rotasi sudah pernah dengar gak tentang Rotasi? Sudah pernah dong. Rotasi biasanya disebut perputaran.
Sebelum memahami materi ini, kamu seharusnya sudah paham apa itu:
Transformasi Geometri Jenis-Jenisnya dan
Translasi dan Refleksi
Rotasi adalah pergeseran atau pemindahan semua titik pada bidang geometri sepanjang busur lingkaran yang memiliki titik pusat lingkaran sebagai titik rotasi.
Perlu diperhatikan:
a. Sudut rotasi bernilai positif apabila dirotasi berlawanan jarum jam,
b. sudut rotasi bernilai negatif apabila dirotasi searah jarum jam
Secara umum, matriks transformasi rotasi dengan sudut  adalah:
adalah:
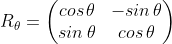
sehingga pemetaan oleh transformasi rotasi dapat dinyatakan sebagai berikut:
1. Transformasi rotasi terhadap pusat O(0,0) dengan sudut rotasi  , ditulis R[O,
, ditulis R[O, ] dirumuskan dengan:
] dirumuskan dengan:
2. Transformasi rotasi terhadap pusat P(a,b) dengan sudut rotasi  , ditulis R[(0,0),
, ditulis R[(0,0), ] dirumuskan dengan:
] dirumuskan dengan:
Untuk memahami penjelasan tentang rumus-rumus di atas, maka perlu sekali kita berlatih menyelesaikan soal-soalnya. Cek selalu di sini !
Jika titik (2,4) dirotasi terhadap titik (0,0) sejauh 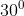 , maka bayangannya adalah....
, maka bayangannya adalah....
Contoh 2:
Jika titik (-4,2) dirotasi terhadap titik O (0,0) sejauh 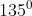 , maka bayangannya adalah....
, maka bayangannya adalah....
Contoh 3:
Jika garis y = 2x+1 dirotasi terhadap titik O(0,0) sejauh 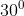 , maka petanya adalah....
, maka petanya adalah....
Contoh 4:
Jika parabola 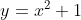 dirotasi terhadap titik A(4,6) sejauh
dirotasi terhadap titik A(4,6) sejauh 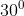 , maka hasilnya adalah....
, maka hasilnya adalah....
Contoh 5:
Jika titik (2,4) dirotasi terhadap titik O (0,0) sejauh 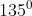 , maka bayangannya adalah....
, maka bayangannya adalah....
Contoh 6:
Jika garis y= 3x dirotasi dengan pusat A(4,2) sejauh 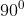 , maka petanya adalah...
, maka petanya adalah...
Contoh 7:
Jika parabola 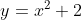 dirotasi terhadap titik pusat A(1,5) sejauh -
dirotasi terhadap titik pusat A(1,5) sejauh -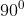 , maka hasilnya adalah....
, maka hasilnya adalah....
Contoh 8:
Bayangan parabola 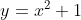 , jika diputar
, jika diputar 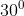 berlawanan arah jarum jam dan pusat (0,0) adalah...
berlawanan arah jarum jam dan pusat (0,0) adalah...
Contoh 9:
Titik B(5,-1) dirotasikan terhadap titik P(2,3) sejauh 90⁰ searah putaran jam. Tentukanlah bayangan titik B tersebut.
Contoh 10:
Jika garis x - 2y = 5 diputar sejauh 90⁰ terhadap titik (2,4) berlawanan arah putaran jam, maka tentukanlah persamaan bayangannya.
Contoh 11:
Bayangan titik A oleh rotasi R(0,45⁰) adalah (-√2,√2). Tentukanlah koordinat titik A.
Contoh 12:
Titik A dirotasikan terhadap titik O(0,0) sejauh 90⁰ berlawanan dengan arah putaran jam. Tentukanlah bayangan titik A.
Untuk pembahasan semua soal, lihat di video ini (segera diupdate ya)
adalah:
, ditulis R[O,
] dirumuskan dengan:

 Editorial Staff
Editorial Staff
0 Comments